For the past few weeks, I have been thinking about pathfinding for our FIRST Robotics team. Specifically, I have been looking into how we could implement a form of spline-based autonomous onto our 2019 robot, Rosetta. There are many libraries available for FIRST teams to use.

FIRST itself has added a PathWeaver application with their 2019 software package to allow us to visually generate trajectories for our robots. Jaci’s Pathfinder is a library that PathWeaver is based in that provided the necessary tools for generating speeds for the motors to go.

In addition, many of the most successful teams, such as Team 254, the Cheezy Poofs, (Yes, that’s their actual name), use splines on their robots. However, Team 254 does many things that would be considered collegiate level, such as writing their own code library that interfaces the hardware directly, using hermetic splines, or calculating custom motion profiles with calculus. The average high schooler usually only begins to know Calculus in their senior year, so the knowledge gap is extremely large.

The Idea

I had a brainwave as I was looking into this. What if there was a system that would generate a spline in realtime to a specific point on the field and cause the robot to follow them with some level of accuracy?

The idea, at the highest level of stratification, can be split into two different sections:

• The Calculation of the Robot Position on the Field (I will refer to it as Sub. 1)
• The Generation and Execution of a Trajectory (Sub. 2)

This idea could be potential fodder for an Innovation Award in FIRST Robotics at competition, if done correctly.

However, to fully execute this idea, I need to grasp the concept of a spline. Such a task will, in my estimation, stretch my mathematical ability to its limits.

Splines

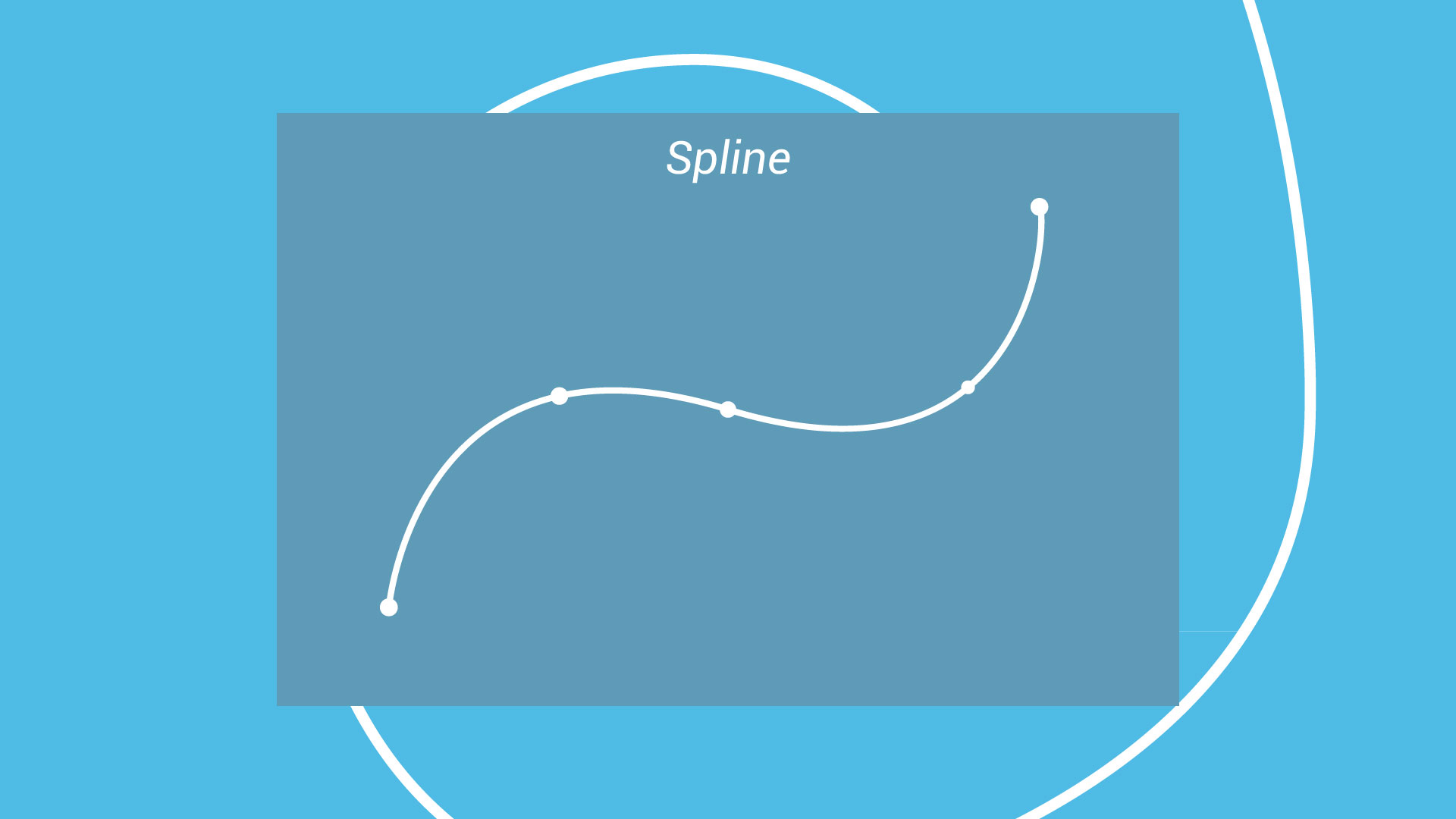
A spline is a unique kind of interpolation. It is, in essence, a kind of polynomial piecewise function, where a polynomial is drawn between two points for a group of points. Unlike regression, which uses a single function, spline interpolation is a system that avoids overfitting due to its complex nature.

How does it create a smooth graph? Well, two polynomials who share a common point must meet a myriad of requirements, one important one being that the derivatives of the two at that point must match. As it has been explained to me, a derivative is the instantaneous speed of a point on a curve. Since this a fundamental calculus principle, I am not currently equipped to calculate a derivative, something I hope to rectify.

Where I Need To Go

In order to create this project, I need to expand my mathematical knowledge to encompass the realms of both Precalculus and basic Calculus. Since I am set up to take Precalculus next year, I will need to make significant headway during the summer. This will most likely consist of practicing with Khan Academy and worksheets I can find online.

Furthermore, I need to reach out to the mentors on my Robotics team for advice and teaching on this area. They can add on to and remove from my project and make it the best it can be. I also will probably contract my best friend Logan O’Neal from Robotics to work with me, as well as Jackson Moody.

This project will be a massive undertaking, one unlike anything I have done in my life before. I need to dedicate myself to this and work as efficently as possible. I am writing this to keep myself accountable, and I hope that those around me can keep myself accountable as well.